Transfer Function Matrix 전달함수 행렬 | (2022-08-29) |
상태방정식 → 전달함수 → 블록선도 | |
▷
Top
▷
전기전자공학
▷
자동제어
▷
상태공간기법
▷
상태공간 표현
1. 상태방정식과 전달함수 간의 관계 ㅇ (상태방정식 표현)[# \mathbf{\dot{x}} = \mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{u} \\ \mathbf{y} = \mathbf{C}\mathbf{x} + \mathbf{D}\mathbf{u} #][# s\mathbf{X}(s) = \mathbf{A}\mathbf{X}(s) + \mathbf{B}\mathbf{U}(s) \\ \mathbf{Y}(s) = \mathbf{C}\mathbf{X}(s) + \mathbf{D}\mathbf{U}(s) #]ㅇ (`상태방정식` → `전달함수 행렬` 형태로 변환) - 상태방정식으로부터 전달함수가 유일하게(Uniquely) 결정됨[# (s\mathbf{I}-\mathbf{A})\mathbf{X}(s) = \mathbf{B}\mathbf{U}(s) \\ \mathbf{X}(s) = (s\mathbf{I}-\mathbf{A})^{-1}\mathbf{B}\mathbf{U}(s) \\ \mathbf{Y}(s) = \mathbf{C}\mathbf{X}(s) + \mathbf{D}\mathbf{U}(s) \\ \quad\quad = \mathbf{C}[(s\mathbf{I}-\mathbf{A})^{-1}\mathbf{B}\mathbf{U}(s)] + \mathbf{D}\mathbf{U}(s) \\ \quad\quad = [\mathbf{C}(s\mathbf{I}-\mathbf{A})^{-1}\mathbf{B} + \mathbf{D}] \mathbf{U}(s) #]- 전달함수 행렬[# \mathbf{T}(s) = \frac{\mathbf{Y}(s)}{\mathbf{U}(s)} = \mathbf{C}(s\mathbf{I}-\mathbf{A})^{-1}\mathbf{B} + \mathbf{D} \\ \qquad\qquad\qquad = \mathbf{C}\frac{\text{adj}(s\mathbf{I}-\mathbf{A})} {\det(s\mathbf{I}-\mathbf{A})}\mathbf{B} + \mathbf{D} #]- 한편, 특성방정식은, 전달함수 분모를 0으로 놓은 것[# \det(s\mathbf{I}-\mathbf{A}) = |s\mathbf{I}-\mathbf{A}| = 0 #]ㅇ (블록선도 표현)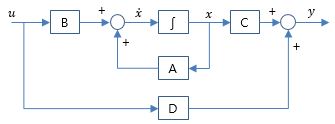
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설][상태공간 표현]1. 상태공간 표현 2. 신호흐름선도,상태선도 3. 상태방정식으로 변환 표현 예 4. 상태방정식→전달함수(전달함수 행렬)
- ▷ Top (분류 펼침) : 1,604개 분류 6,618건 해설