Vector Function Derivative 벡터 함수 미분, 벡터 함수 도함수, 벡터 미분 | (2024-11-14) |
스칼라장의 미분, 스칼라장의 도함수, 벡터장의 미분, 벡터장의 도함수, Jacobian Matrix, 야코비 행렬 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
벡터해석학
1. 벡터 함수의 미분 (또는 도함수) ㅇ 벡터함수 내 각 성분함수를 미분함으로써 얻어지는 벡터함수[# \mathbf{r}(t) = f(t)\hat{\mathbf{i}} + g(t)\hat{\mathbf{j}} + h(t)\hat{\mathbf{k}} = \; < f(t),g(t),h(t) > \\ \qquad x = f(t), y = g(t), z = h(t) \\ \; \\ \frac{d\mathbf{r}(t)}{dt} = \mathbf{r}'(t) \\ \qquad\; = \lim_{\Delta t\to 0}\frac{\mathbf{r}(t+\Delta t)-\mathbf{r}(t)}{\Delta t} \\ \qquad\; = \left( \frac{df(t)}{dt}\hat{\mathbf{i}} + f(t)\frac{d\mathbf{i}}{dt} \right) + \left( \frac{dg(t)}{dt}\hat{\mathbf{j}} + g(t)\frac{d\mathbf{j}}{dt} \right) + \left( \frac{dh(t)}{dt}\hat{\mathbf{k}} + h(t)\frac{d\mathbf{k}}{dt} \right) \\ \qquad\; = \frac{df(t)}{dt}\hat{\mathbf{i}} + \frac{dg(t)}{dt}\hat{\mathbf{j}} + \frac{dh(t)}{dt}\hat{\mathbf{k}} \\ \qquad\; = < f'(t),g'(t),h'(t) > #]ㅇ 이렇게 얻어진 `벡터함수의 미분(도함수)`는, - r(t)로 정의되는 곡선의 어떤 점에서의 `접선 벡터(Tangential Vector)`가 됨 - 이를 `속도 벡터(Velocity Vector)` 라고도 함 ㅇ 다변수 벡터함수의 미분을 행렬로 표기 : 야코비안/자코비안 행렬, 야코비 행렬 (Jacobian Matrix)[# F'(P) = \frac{∂F(f_1,\cdots,f_m)}{∂(x_1,\cdots,x_n)} (P) \\ \qquad = \begin{bmatrix} \dfrac{∂f_1}{∂x_1}(P) & \dfrac{∂f_2}{∂x_2}(P) & \cdots & \dfrac{∂f_1}{∂x_n}(P) \\ \dfrac{∂f_2}{∂x_1}(P) & \dfrac{∂f_2}{∂x_2}(P) & \cdots & \dfrac{∂f_2}{∂x_n}(P) \\ \vdots & \vdots & \vdots & \vdots \\ \dfrac{∂f_m}{∂x_1}(P) & \dfrac{∂f_m}{∂x_2}(P) & \cdots & \dfrac{∂f_m}{∂x_n}(P) \end{bmatrix} #]- [참고] 야코비(Karl Jacobi, 1804–1851) : 독일의수학자 2. 벡터 미분의 물리적 의미 => 물체의 운동 표현 ※ 공간,평면 영역에서 움직이는 물체의 운동(속도,가속도,회전 등) 표현 - [직각좌표계 표현] ☞ 속도벡터,가속도벡터 참조 - [극좌표계 표현] ☞ 원운동 벡터 표현 참조 ㅇ 회전하는 벡터함수의 시간 미분 및 그 성질(의미)- 벡터의 크기가 일정(dA/dt=0)하고 방향 만 변하면, . 원래 벡터의 수직인 벡터가 됨 즉,
3. 벡터 함수의 미분 공식 ㅇ 상수 벡터의 미분 :
[# \frac{d}{dt} \mathbf{c} = \mathbf{0} #]ㅇ 벡터의 스칼라 곱셈의 미분 :[# \frac{d}{dt} [c\,\mathbf{r}(t)] = c\,\mathbf{r}'(t) #]ㅇ 스칼라함수,벡터함수 곱의 미분 :ㅇ 벡터함수 합의 미분 :
ㅇ 벡터함수 내적의 미분 :
ㅇ 벡터함수 외적의 미분 :
ㅇ 벡터함수의 연쇄법칙 :
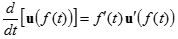
▷벡터해석학
1. 벡터 해석학 2. 벡터 함수 3. 벡터 함수 미분 4. 위치/속도/가속도 벡터 5. 원운동 벡터 표현 6. 주요 벡터공식 7.
▷스칼라장,벡터장 연산
8.
▷적분 정리
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설] 후원[벡터해석학]1. 벡터 해석학 2. 벡터 함수 3. 벡터 함수 미분 4. 위치/속도/가속도 벡터 5. 원운동 벡터 표현 6. 주요 벡터공식 7. [스칼라장,벡터장 연산] 8. [적분 정리]
- ▷ Top (분류 펼침) : 1,604개 분류 6,618건 해설